“MUOIONO GLI IMPERI,
I TEOREMI DI EUCLIDE CONSERVANO
ETERNA GIOVINEZZA”.
La Biologia è spesso considerata una scienza meno predittiva rispetto alle scienze “dure” come Fisica, Chimica o Ingegneria. Effettivamente, nell’Ottocento gli studi di Biologia consistono perlopiù nel raccogliere campioni e sezionare animali. I modelli basati sulla teoria di Darwin sono in grado di spiegare il perché della situazione esistente, ma poco utili per predire l’evoluzione futura. Nei primi anni del Novecento, però, anche i matematici cominciano ad interessarsi allo studio degli esseri viventi, sviluppando una nuova branca della biologia con esiti sorprendenti.
Fra questi Vito Volterra, un grande italiano che contribuì a sviluppare la biologia matematica e che ebbe un ruolo importante nella scienza e nella storia d’Italia. Fu infatti senatore, antifascista, perseguitato politico; un uomo a cui sono particolarmente grato perché fondatore dell’istituzione per cui mi onoro di lavorare, il Consiglio Nazionale delle Ricerche.
Volterra nasce nel 1860 ad Ancona, di famiglia poverissima; riesce a studiare solo grazie all’aiuto di suo zio e del suo professore di fisica, che vedono in lui un grande talento. Hanno ragione: a 19 anni Volterra è ammesso alla normale di Pisa, si laurea a 22 anni, diventa professore di Meccanica Razionale a 23, poi socio dell’Accademia dei Lincei. Nel 1905 è eletto senatore del Regno d’Italia. È uno scienziato famoso ma anche un fervente patriota; allo scoppio della Prima guerra mondiale si arruola nell’esercito, nonostante i suoi 55 anni. Lavora allo sviluppo di una nuova tecnologia, i dirigibili, e per primo ha l’idea di sostituire l’idrogeno, infiammabile ed esplosivo, con l’elio. Dopo la guerra diventa presidente dell’Accademia dei Lincei. Fonda nel 1923 il Consiglio Nazionale delle Ricerche, con lo scopo di riunire i diversi centri e uffici che fanno ricerca in Italia.
La figlia, Luisa, è corteggiata da un giovane biologo dalmata, Umberto D’Ancona, e i due si sposano nel 1926. Umberto si occupa di studiare la pesca in Adriatico, ed ha un problema: i pescatori di Fiume si lamentano con lui perché, dopo la guerra, pescano meno pesce pregiato e tanto pesce di poco valore, soprattutto squali e razze. La cosa sorprende perché durante la guerra la pesca è stata quasi nulla, quindi ci si aspetterebbe un aumento delle specie di pesce azzurro più pregiate.
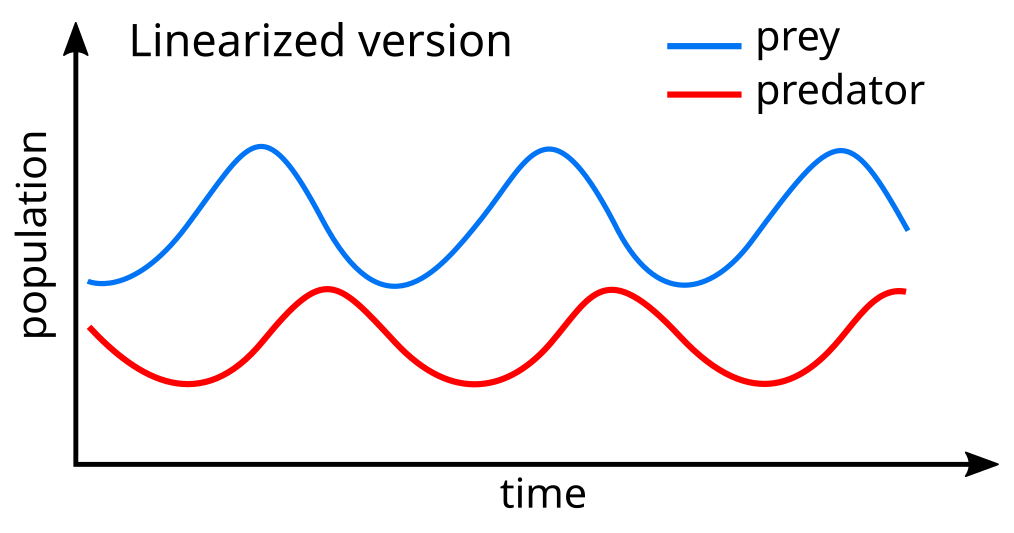
Volterra decide di usare la matematica risolvere il problema di suo genero. Immagina un ecosistema semplificato in cui ci sono solo due specie, una di prede, l’altra di predatori. Volterra usa due equazioni differenziali per simulare l’andamento di questo ecosistema: in assenza di predatori, le prede si moltiplicano all’infinito; in assenza di prede, i predatori si estinguono. Il sistema oscilla periodicamente tra diverse fasi:
1) le prede si moltiplicano;
2) l’abbondanza di prede fa aumentare, con un certo ritardo, il numero di predatori;
3) i tanti predatori decimano le prede, il cui numero torna così al valore iniziale.
Il ragionamento in sé sembra abbastanza semplice, ma l’analisi matematica permette di arrivare a conclusioni sorprendenti. Pescando in maniera uniforme sia predatori che prede, l’effetto finale sarà un aumento del numero delle prede! La pesca moderata prima della guerra, quindi aiutava a tenere alto il numero di pesce pregiato; è stato proprio il blocco alla pesca causato dalla guerra a causare l’aumento dei predatori, squali e razze.



Un’altra conclusione sorprendente è che, se ci sono due specie di predatori che si contendono esattamente la stessa preda, non può esserci equilibrio stabile tra i due; alla lunga, solo una delle due specie può sopravvivere. Volterra non è il primo a sviluppare questo modello, è preceduto da un matematico americano, Alfred Lotka, ma Volterra dimostra la validità del modello applicandolo a un caso reale, i dati di suo genero, per questo i suoi articoli hanno più impatto di quelli dell’americano.
Da allora le equazioni di Lotka-Volterra, pur molto schematiche, sono state applicate con successo a sistemi anche complessi, con più di due specie in competizione tra loro tramite interazioni complesse. Ma anche in presenza di limiti delle risorse alimentari o altre varianti, riuscendo a chiarire anche sistemi reali come, ad esempio, il controllo della dannosa cocciniglia e del suo coccinella.
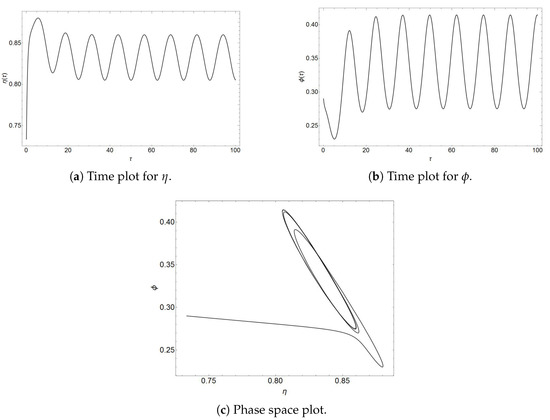
La Scienza prende sempre direzioni inaspettate; è sorprendente come, parafrasando il premio nobel E. Wigner, la matematica abbia un “irragionevole” efficacia nello spiegare le leggi della Natura. A dicembre del 2021, una ricerca pubblicata sulla rivista Photonics ha usato le equazioni di Volterra, pensate per la biologia, per qualcosa di completamente diverso, cioè la dinamica dei raggi laser, spiegata come una competizione tra i predatori (i fotoni) e le prede (gli elettroni).
La storia umana di Volterra non finisce bene. Con l’ascesa del Fascismo, lo scienziato di successo diventa inviso al potere. Nel 1927 perde la presidenza del CNR che passa a Guglielmo Marconi, scienziato favorevole al nuovo regime. Nel 1931 il regime impone a tutti i professori universitari di giurare fedeltà al Fascismo e in tutta Italia, solo dodici docenti (dodici!) si rifiutano; Volterra è uno di loro. Viene espulso dall’Università e dall’Accademia dei Lincei, costretto ad espatriare in Francia e poi in Spagna.
Volterra muore nel 1940; nessuna delle istituzioni che ha fondato o diretto può celebrarlo, a causa della censura politica. Solo la Pontificia Accademia delle Scienze, di cui era rimasto membro, ne terrà una breve commemorazione.
Sulla sua tomba, fa scrivere la frase:
“MUOIONO GLI IMPERI, MA I TEOREMI DI EUCLIDE CONSERVANO ETERNA GIOVINEZZA”.
Questa frase è sopravvissuta al regime fascista allora imperante, e ancora valida nei drammatici momenti che stiamo vivendo.
Clicca sull’immagine qui sotto per vedere l’evoluzione predatori/prede in tempo reale.
Link utili:




